How to employ statistical approaches to identify differentially expressed genes (DEG)

Identifying differentially expressed genes (DEGs) is an important task in genetic research because it allows researchers to identify genes that are associated with a particular phenotype or condition of interest. DEGs are genes that show significant differences in expression levels between two or more groups, such as a disease group and a healthy control group. The identification of DEGs can have a variety of significant ramifications, including:

1.Understanding disease mechanisms: DEGs can provide insights into the molecular mechanisms underlying a particular disease or phenotype.
2.Biomarker discovery: DEGs can also be used as biomarkers for diagnosis or prognosis of a disease.
3.Personalized medicine: DEGs can also be used to identify patient subgroups that may respond differently to a particular treatment.
4.Drug development: DEGs can also be used as targets for drug development.

The identification of DEGs is a critical step in genetic research as it allows researchers to gain insights into the molecular mechanisms underlying a particular phenotype or condition and potentially identify new targets for diagnosis, treatment, and drug development.

Adopted Statistical methods for DEGs identification

In simple words, if some changes in gene expression levels are observed between two experimental conditions or we see a statistically significant difference in the read counts, it is indicated as Differential gene expression (DEG). we can say that checking the difference in the mean value of gene expression under different conditions, is sufficient.
However, practically expression of gene mostly has a normal distribution. It is not easy to determine the differential gene expression by a simple comparison of means and variance.

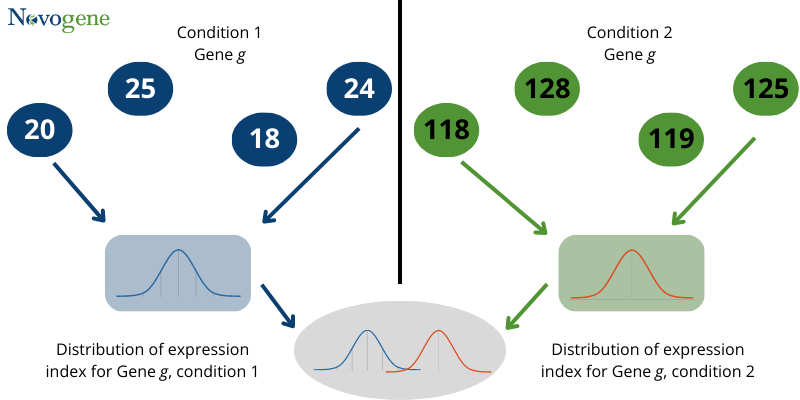Fig1: Distribution of differential expression statistic

Therefore, in order to identify the difference in gene expression between two conditions, it is crucial to find the statistical distribution properties. These statistical distribution properties can be used to approximate the differentially expressed genes. Parameters like p-value, p-adjust, q-value and other indicators are used to determine whether a gene has differential expression or if there is a false positive error. p-value or probability-value describes how likely you can find a particular set of observations, if the null hypothesis of the data was true. p-adjust value is the adjustment made to correct P-values. q-value is a value used to determine False Discovery Rate (FDR); q-value attempts to control the percentage of false positives among a collection of scores.

For example, sometimes there are many 0 values in the read counts of transcripts of our samples. This situation will have an impact on the reliability of p-value, because most of the times the p-value will be significant. However, we can’t say that this is always very realistic. In this case we need to correct the p-value. The p-adjust value is calculated first to correct the p-value. Although the details of the complete correction process are not discussed here, we can simply say that to determine the credibility of p-value, the parameter used is p-adjust. It comes from the p-value, but it is more credible relative to the p-value.
In conclusion, we know that when both p-value and p-adjust are available, we should choose p-adjust to be used as the threshold of significance, as it is more credible.

The corrected p-value is used to determine the significance of gene difference, between two samples. The smaller the corrected p-value, the more significant the difference.
We can also use |log2Foldchange| to determine the size of the difference. The larger the |log2Foldchange|, the greater is the difference multiplicity. However, the screening of differential genes is based on statistical significance. It is not logical to judge whether a gene is differential or not by the size of two values.
(1) Firstly, the read counts of some samples are affected by the depth of sequencing. The read counts may be higher due to the sequencing depth.
(2) Secondly, during the analysis of variance, the distribution of read counts need to be estimated. The analysis of previous experience shows that read counts obey the negative binomial distribution. In the case of replicates, their quality also has an impact on the difference between genes. If the replicates are poor, the within-group variation (variation due to error) will mask out some of the between-group variation (variation due to the factor). After the parameter’s estimation, a specific test is needed to determine whether the difference is genetic or not.
(3) As explained earlier, after the calculation of p-value, it needs to be corrected by multiple hypothesis testing to reduce false positives.

In the multiple hypothesis testing process, the q-value is the expected value of the number of false rejections (rejection of the true hypothesis (null hypothesis). It is a proportion of all rejected hypotheses (which represents the error rate) in the multiple hypothesis testing process. q-value can be defined as the probability of false positives for p-value, when q-value < 0.05, the significant false positive for p-value is less than 0.05. To summarize we can say that both the p-value and q-value are statistical test variables. For any gene difference, the lowers the p-value/q-value, the lower will be the probability of a false positive result and the higher will be the reliability. However, q-value is more stringent than p-value. When the number of differential gene results is low, p-value based screening can be used as a second-best option. On the other hand, the q-value based screening may filter out a small number of different genes. However, comparing to the majority of false positives and the small probability of true positives, the loss of all these true positives is not very important.